Growth Algorithms

Sep 2019

Along with fractals, I also got really into growth algorithms, especially making them run in realtime. It seems like a perfect intersection of design and art with computer science and math.

Here are various realtime versions of some interesting growth algorithms I have seen over the years.

Mesh based
Mesh Splitting / Spring and attractive forces
- Diffusion-Limited Aggregation
Voxel based
Gray-Scott
Anisotropic Dendritic Solidification

Mesh Based

These involve splitting a manifold (1d or 2d surface) and then moving the nodes around in a higher dimensional space to minimise overlap

The simplest version is a line, which can be split and curved to remove intersections:

from Anders Hoff (inconvergent)

You can also split a mesh, it is just more complicated:

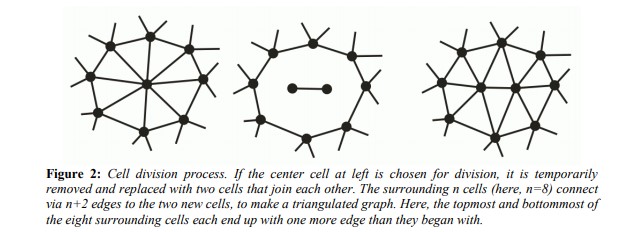From Growth Forms, George Hart 2009

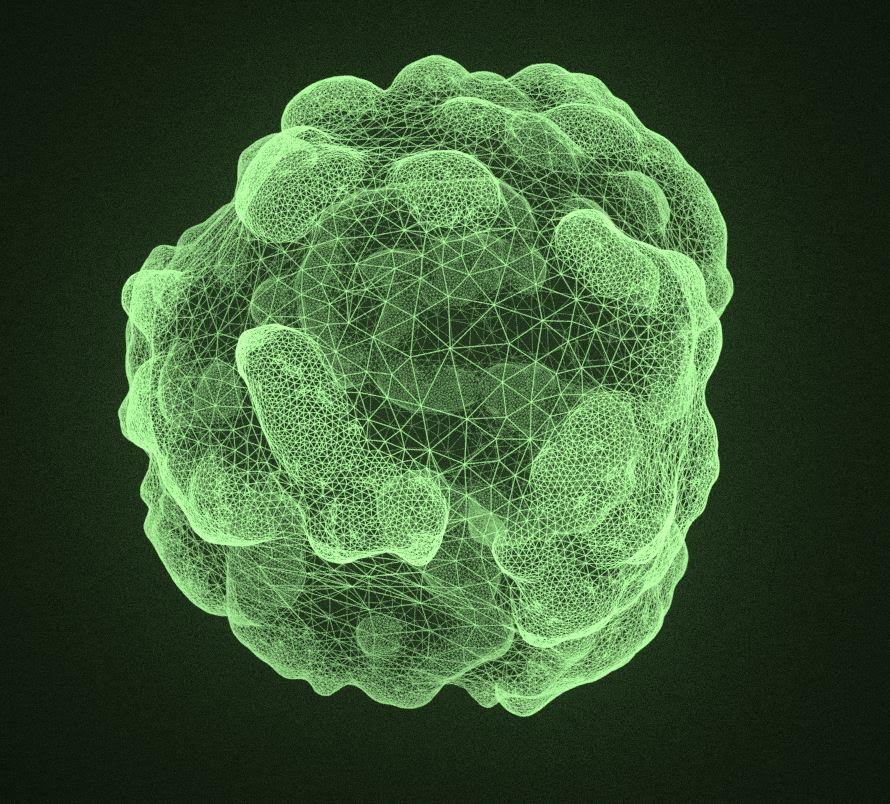
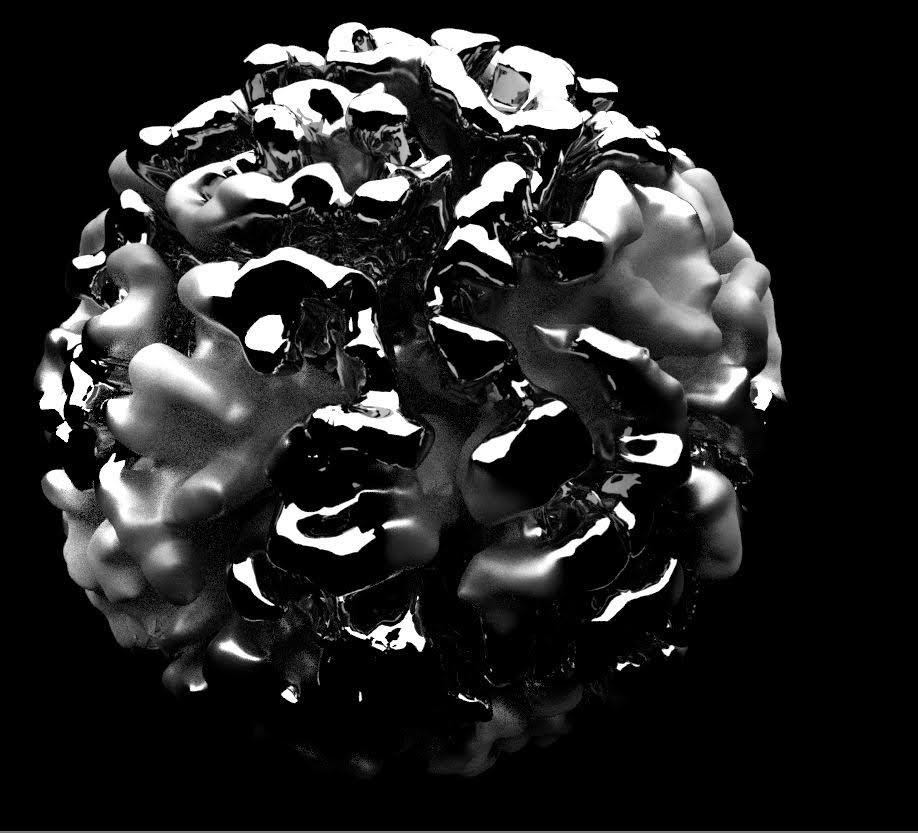
Mesh generated in unity, wireframe rendered in Blender

This was based on mxsage cpp implementation of Andy Lomas.

I implemented it in a unity compute shader, but graph data structures are pretty tricky to implement on GPU. My version could only get about this big before something started bugging out and I never fixed it. oh well, this isn’t really the most elegant method anyways.

Diffusion Limited Aggregation

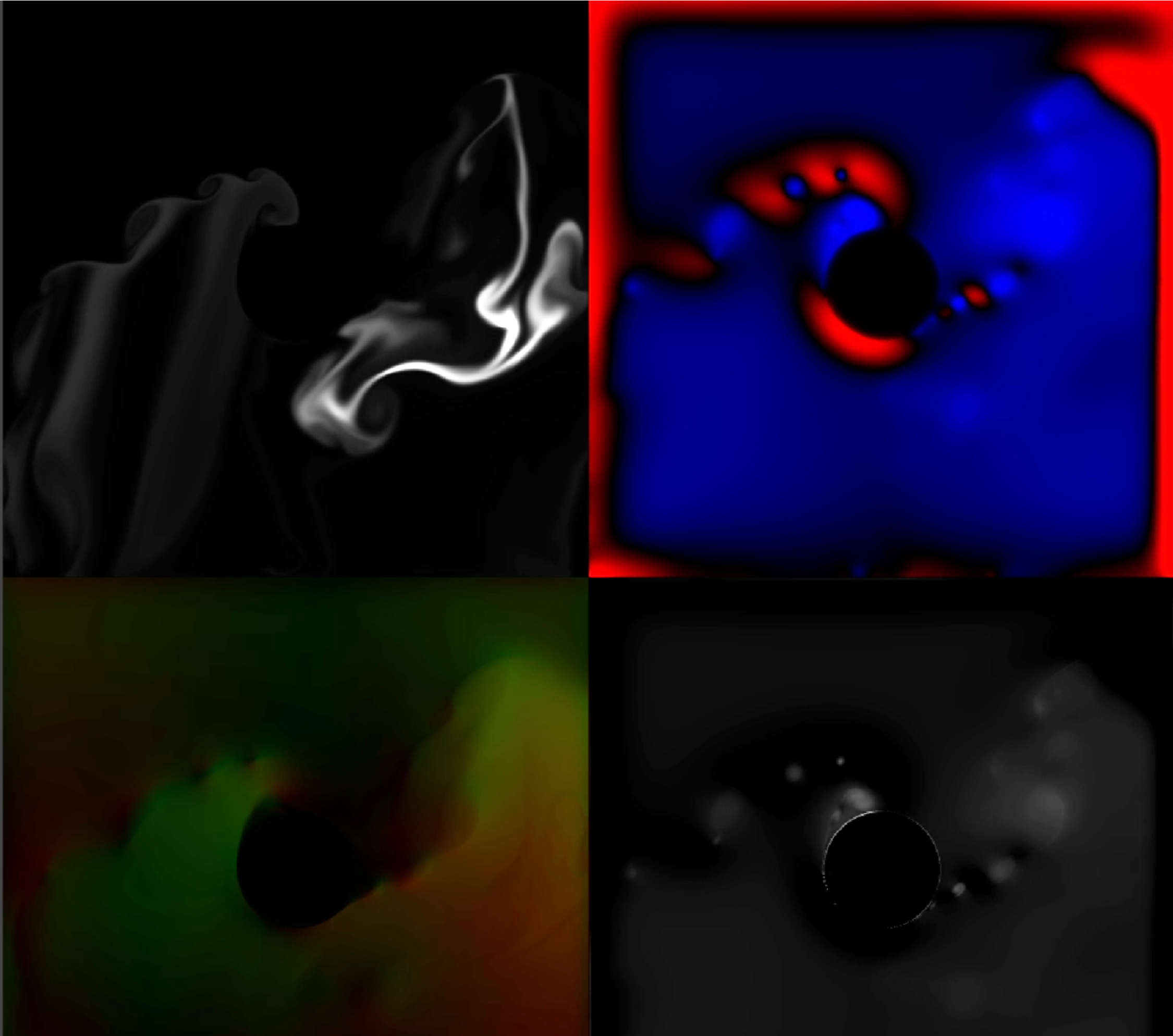
DLA is a way to generate branching structures. It simulates particles moving around and then depositing themselves on a surface, which grows.

There was no advection here, just random particle movement. This uses unity sopheres and colliders, which got quite slow as unity only supoorts around 10,000 colliders maximum.

These particles were advected using divergence-free curl noise

This is DLA running in a voxel grid in realtime in Unity, making it a hybrid of the next approach.

There are particles moving through a volume and depositing when they hit a cell with a threshold. The volume is being diffused a bit over time, so it looks like it’s melting and smoothing a bit. An isosurface is rendered with marching cubes and colored based on the laplacian (curvature) of the scalar field.

Voxel Based

I like thhis a lot more because the equations are very simple and GPUs are fast at doing 3D texture updates with compute shaders.

This technique computes scalar fields and updates them with some differential equations. the most well known is probably turing patterns, using gray scott equations. These generalize to 3D

live demo

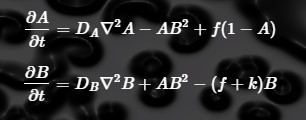
Dendritic solidification, Laplacian growth

I was intrigued by Nervous System and wondered how to implement this in real time using compute shaders.

They just showed these equations briefly at the beginning of a video once

Eventually I found this paper Ryo Kobayashi 1994 with a similar equation. notably the m is now dependeat on the temperateure and gradient of the phase field, creating anisotropic growth.

The simulation works by storing the temperature and phase of each cell of the grid. The temperature spreads out (dT), according to the phase change of neighboring cells. Heat is absorbed at the solid/liquid boundary to The phase changes (dp) similar to a traveling wave along the interface In this case liquid would be phase=0, solid phase=1